Product Operator

The product operator formalism is a quantum mechanical method used to describe the outcome of NMR pulse sequences. It allows the prediction of the behaviour of the bulk magnetisation as it evolves under the action of pulses and delays. It is a simplification of the density matrix formalism but allows prediction of results that are not possible using the simple vector model. The product operator is described in full by James Keeler here and in video format here.

For a single spin with nuclear spin of ½ there are four base operators: I_x, I_y, I_z (which represent the x-, y- and z-components of magnetisation) and ^E/₂ representing the unity operator.

Rotations around each axis follow the patterns below.

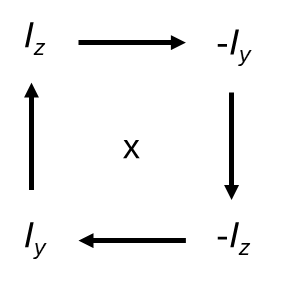
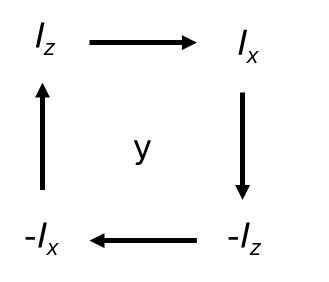
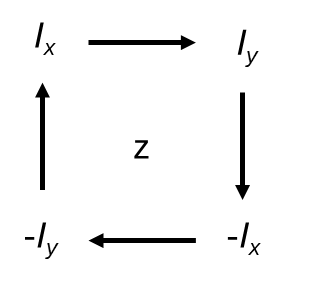
So a RF pulse with an rotational angle of φ along the x-axis would have the following equation:

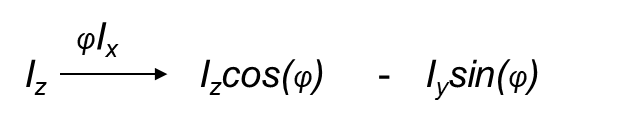
If φ = 90° (^π/₂) then the result will be -Iy as cos(^π/₂) = 0 and sin (^π/₂) = 1.

Similarly an RF pulse with an rotational angle of φ along the y-axis would have the following equation:

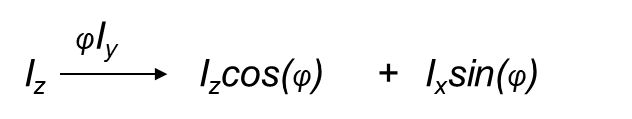
If φ = 90° (^π/₂) then the result will be Ix.

For rotations around the z-axis the operator is the chemical shift in Hertz (ω) with respect to time (τ).

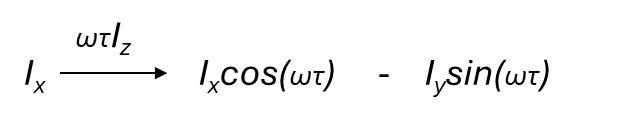
The product operator model is ideal when studying coupled spin systems which are insufficiently explained by the vector model. This is clearly demonstrated when looking at heteronuclear systems. The two spins are here labelled I and S. The two spins evolve in the same way as for isolated spins for pulses and chemical shift but have to applied separately so rotations of the I spin do not affect the S spin and vice versa. Evolution due to the couplings between the I and S spins are not independent and so we need a new term to describe their relationship. The pattern of evolution due to coupling is therefore:

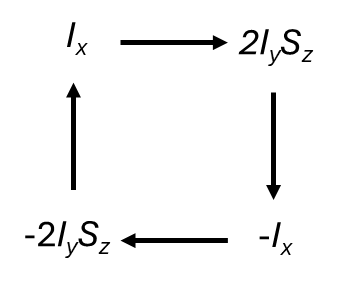
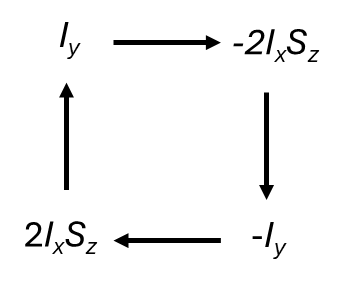
With the equations being:

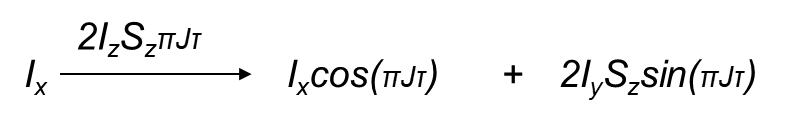
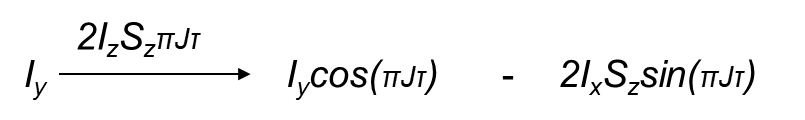
When working through pulse sequences using product operators it is often useful to simplify the terms. The following relationships are valuable tools to aid this process.

cos2(α) + sin2(α) = 1
cos(−α) = +cos(α)
sin(−α) = −sin(α)
cos(α + β) = cos(α) cos(β) − sin(α) sin(β)
cos(α − β) = cos(α) cos(β) + sin(α) sin(β)
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α − β) = sin(α) cos(β) − cos(α) sin(β)